Compressed Air Energy Storage - CAES

In pumped storage power plants, electricity is stored as potential energy in two storage reservoirs located at different heights. The stored energy is:

E = m.g.Δh = ρ.V.g.Δh = V.Δp

Here, m is the mass of water used for storage, g is the acceleration due to gravity, and Δh is the difference in height of the storage reservoirs. The mass of the water is the product of the density ρ and the volume V, and thus the stored energy can be expressed as the product of the volume and the pressure difference Δp.

The energy content or work stored in compressed air is w = pΔV, thus physically similar to the energy in pumped storage.

According to the 1st law of themodynamics, the internal energy of the gas:

E = ΔU = q + w

This means that whenever work is done on a gas or the gas does work, the heat content of the gas also changes.

The Problem 

The generation of heat during the compression of a gas is the main problem in compressed air storage. In previous adiabatic compressed air storage, the assumption is that this heat is stored above ground and then returned to the process during expansion, thus achieving an efficiency of over 70%. Temperatures reach 500 °C. One example of this is the publicly funded ADELE project.

However, this efficiency can hardly be achieved because the heat and the associated high temperature are not only generated above ground during compression and expansion. The storage cavern would also cool down considerably during expansion, which would lead to high geomechanical stress and would not be permissible in conventional natural gas storage technology.

It is further generally the case that heat cannot be completely converted to work in a thermodynamic process. The efficiency depends on the temperature ratio and is very low in the case of adiabatic expansion as in ADELE

.η = T1 / T2 = 300/800 = 0.375

The Reason

The temperature change during an adiabatic compression or expansion depends on the pressure ratio. 

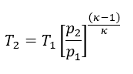
Thus, for a pressure increase from 0.1 bar to 1 bar, the temperature change is the same as from 1 to 10 bar. This is shown in the diagram below for a diatomic ideal gas and would also apply to air (the initial temperature T1 is 300 K). At a compression ratio of 100, the temperature would increase by approx. 800 °C.

Temperature changes during adiabatic compression as a function of the compression ratio

.

The Solution

Since the stored pressure energy corresponds to the product of pressure and volume pV, the same energy is contained in a compression from 1 to 70 bar, as under the operating conditions of the ADELE accumulator, as in a compression from 100 to 170 bar, but the temperature increase would be only 50 °C instead of 500 °C. This can be achieved if the air is taken from a second storage chamber instead of from the atmosphere.

This can be achieved if the air is taken from a second storage chamber instead of from the atmosphere. Technically, this can be implemented without great effort, the heat can be easily stored in a water reservoir and the efficiency would be:

η = T1 / T2 = 300 / 350 = 0.857

erneo compressed air storage system with two storage caverns